Ncert Maths Book Solution Class 10 Chapter 6
Practice Test - MCQs test series for Term 1 Exams
NCERT Solutions for Class 10 Maths Chapter 6 - Triangles
NCERT Solutions for CBSE Class 10 Maths make learning mathematics simple and scoring. Students can access NCERT Solutions for CBSE Class 10 Maths at any point in time. The following list of contents make a complete package of Topper Learning's study material assuring perfect preparation:
- CBSE Class 10 Maths Doubt Solver
- CBSE Class 10 Maths Video Lessons
- CBSE Class 10 Maths sample papers
- CBSE Class 10 Maths Undoubt
- CBSE Class 10 Maths Most Important Questions
- CBSE Class 10 Maths Past Year Papers
- CBSE Class 10 Maths Textbook Solutions
- CBSE Class 10 Maths Revision Notes
Thus we leave no stones unturned to boost your scores. Increase your confidence by practising using NCERT solutions for CBSE Class 10 Maths.
NCERT Solutions for Class 10 Maths Chapter 6 - Triangles
In your earlier classes, you have learnt about Triangle and its properties. In this chapter, we shall be studying about two figures that may have the same shape but not the same size. This chapter will introduce you to the concept of the similarity of triangles. Here are the following key points discussed in this chapter:
- What are similar figures?
- Similarity of Triangles
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Pythagoras Theorem
Students are often puzzled by complex questions from this chapter. Reduce all these complexities with in-depth and elaborate NCERT solutions for CBSE Class 10 Maths. TopperLearning's conceptual insight and stepwise solutions make Mathematics Chapter Triangles
very easy and scoring for students. Given below are solutions for each question from all the exercises in Class 10 Maths Chapter Triangles.
CBSE Class 10 Mathematics Chapter 6 - Triangles Exercise Ex. 6.1
Understand what are similar figures with Class 10 Maths Chapter Triangles. This exercise from Maths Chapter Triangles tells us that all congruent figures are similar but the similar figures need not be congruent. There are some concept-based questions asked in this exercise answers to which are available on Triangles NCERT solutions. Such questions are popular in the category of multiple-choice questions. Explore and practise more questions with CBSE Class 10 Maths study material. TopperLearning's CBSE Class 10 Maths Textbook solutions help you in accessing your solutions whenever you need them.
CBSE Class 10 Mathematics Chapter 6 - Triangles Exercise Ex. 6.2
What can you say about the similarity of two triangles? What are the conditions for the similarity of two triangles? The answers to these questions are provided with apt methodology as accepted by the CBSE board by our subject experts in Triangles NCERT solutions. Refer to NCERT solutions for CBSE Class 10 Maths for answers to every question from the textbook. Students are advised to go through CBSE Class 10 Maths video lessons
CBSE Class 10 Maths sample papers, CBSE Class 10 Maths most important questions, CBSE Class 10 Maths past year papers and CBSE Class 10 Maths revision note for all-around preparation. Students can tally their solutions and use our doubt solver "Undoubt" feature in case of doubts.
CBSE Class 10 Mathematics Chapter 6 - Triangles Exercise Ex. 6.3
Increase your knowledge in Maths Chapter Triangles by understanding the criteria for the similarity of triangles. Solve all the questions from Class 10 Maths Chapter Triangles Exercise 6.3 and refer to Triangles NCERT solutions to check your solutions. Learn all the basic theorems for similarity with TopperLearning's CBSE Class 10 Maths video lessons. This exercise hand some important questions which can be checked in CBSE Class 10 Maths most important questions. Boost your confidence by taking tests and gain full clarity.
CBSE Class 10 Mathematics Chapter 6 - Triangles Exercise Ex. 6.4
The concept of similarity is useful in calculating the area of triangles. Understand how extensively explained video solutions available at CBSE Class 10 Maths video lessons. Apply this concept in the questions from Mathematics Chapter Triangles Exercise Ex. 6.4 and check your solutions with CBSE Class 10 Maths Textbook solutions. Topperlearning's study material explains the method of writing answers with proper conceptual insight. NCERT Solutions for CBSE Class 10 Maths helps not only in gaining clarity but also increases your scores, Assess your knowledge with CBSE Class 10 Maths past year papers and CBSE Class 10 Maths sample papers at your convenience.
CBSE Class 10 Mathematics Chapter 6 - Triangles Exercise Ex. 6.5
You are already familiar with the Pythagoras Theorem from your earlier classes. You
had verified this theorem through some activities and made use of it in solving certain
problems. You have also seen proof of this theorem in Class IX. Now, we shall prove
this theorem using the concept of similarity of triangles. In proving this, we shall make use of a result related to the similarity of two triangles formed by the perpendicular to the hypotenuse from the opposite vertex of the right triangle.
TopperLearning's Triangles NCERT solutions explain the theorem as well the examples associated with it in the simplest manner possible. Refer to CBSE Class 10 Maths study material anytime and get everything that you need. The questions from this exercise are often asked in the 3-4 mark category. Explore CBSE Class 10 Maths sample papers, CBSE Class 10 Maths most important questions, CBSE Class 10 Maths past year papers and attempt all the most important questions.
CBSE Class 10 Mathematics Chapter 6 - Triangles Exercise Ex. 6.6
TopperLearning's study material is an asset for every 10th grader. We not only help you with the main exercise but option optional exercise like this one. All the solutions from this exercise are available at NCERT solutions for CBSE Class 10 Maths. Extend your limits and attempt questions from this exercise and check your solutions with Triangles NCERT solutions. Refer to video solutions and most important questions at any hour and let there be no hurdles in your preparation. Although this exercise is optional, it is always wise to have a look at the questions and tally your solutions. Clear all your doubts with our special feature "Undoubt" where all your doubts will be catered by our team of subject experts.
Readmore
Updated NCERT Textbook Solutions Coming Soon!
Chapter 6 - Triangles Exercise Ex. 6.1
Solution 1
(i) All circles are SIMILAR.
(ii) All squares are SIMILAR.
(iii) All EQUILATERAL triangles are similar.
(iv) Two polygons of same number of sides are similar, if their corresponding angles are EQUAL and their corresponding sides are PROPORTIONAL.
Solution 2
(i) Two equilateral triangles with sides 1 cm and 2 cm.
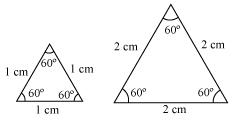
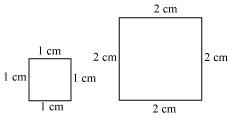
Two squares with sides 1 cm and 2 cm
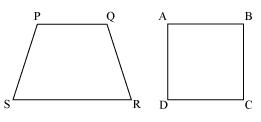
(ii) Trapezium and Square
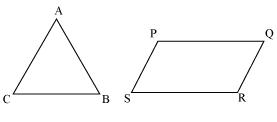
Triangle and Parallelogram
Solution 3
Quadrilateral PQRS and ABCD are not similar as their corresponding sides are proportional i.e. 1:2 but their corresponding angles are not equal.
Chapter 6 - Triangles Exercise Ex. 6.2
Solution 1
(i)

Let EC = x
Since DE || BC.
Therefore, by basic proportionality theorem,

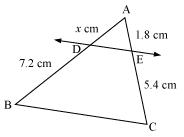
Let AD = x
Since DE || BC,
Therefore by basic proportionality theorem,

Solution 2
(i)
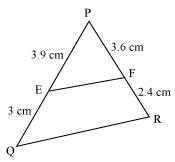
Given that PE = 3.9, EQ = 3, PF = 3.6, FR = 2.4
Now,

(ii)
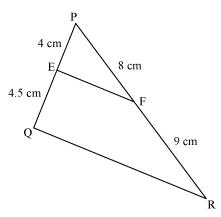
PE = 4, QE = 4.5, PF = 8, RF = 9

(iii)
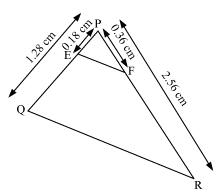
PQ = 1.28, PR = 2.56, PE = 0.18, PF = 0.36

Solution 3
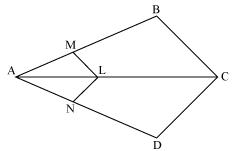
In the given figure
Since LM || CB,
Therefore by basic proportionality theorem,
Solution 6
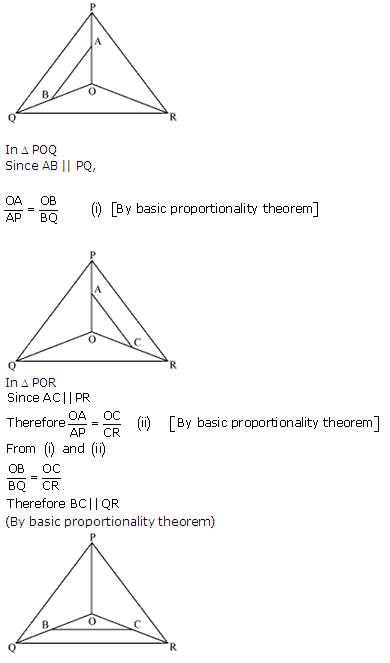
Solution 7

Consider the given figure
PQ is a line segment drawn through midpoint P of line AB such that PQ||BC
i.e. AP = PB
Now, by basic proportionality theorem

i.e. AQ = QC
Or, Q is midpoint of AC.
Solution 8
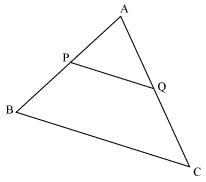
Consider the given figure
PQ is a line segment joining midpoints P and Q of line AB and AC respectively.
i.e. AP = PB and AQ = QC
Now, we may observe that
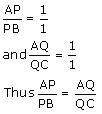
And hence basic proportionality theorem is verified
So, PQ||BC
Solution 9

Solution 10
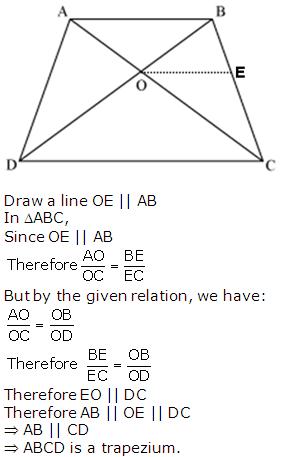
Chapter 6 - Triangles Exercise Ex. 6.3
Solution 4
In ![]() PQR
PQR
![]() PQR =
PQR = ![]() PRQ
PRQ
Therefore PQ = PR (i)
Given,

Solution 10
and![]() ACD =
ACD =![]() FGH
FGH
Therefore![]() DCA ~
DCA ~![]() HGF (by SAS rule)
HGF (by SAS rule)
Solution 14

Solution 15
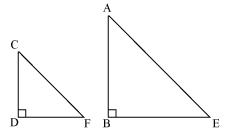
Let AB be a tower
CD be a pole
Shadow of AB is BE
Shadow of CD is DF
The light rays from sun will fall on tower and pole at same angle and at the same time.
So, ![]() DCF =
DCF = ![]() BAE
BAE
And ![]() DFC =
DFC = ![]() BEA
BEA
![]() CDF =
CDF = ![]() ABE (tower and pole are vertical to ground)
ABE (tower and pole are vertical to ground)
Therefore ![]() ABE ~
ABE ~ ![]() CDF
CDF
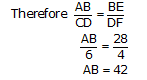
So, height of tower will be 42 meters.
Chapter 6 - Triangles Exercise Ex. 6.4
Solution 1

Solution 4
Let us assume two similar triangles as ![]() ABC ~
ABC ~ ![]() PQR
PQR

Solution 5

Since D and E are mid points of ![]() ABC
ABC

Solution 8
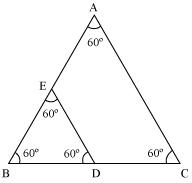
We know that equilateral triangles are having all its angles as 60º and all its sides of same length. So, all equilateral triangles are similar to each other. So, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
Let side of ![]() ABC = x
ABC = x
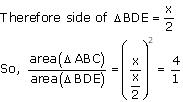
Solution 9
If, two triangles are similar to each other, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
Given that sides are in the ratio 4:9.
Hence, (d).
Chapter 6 - Triangles Exercise Ex. 6.5
Solution 1
i.Given that sides are 7 cm, 24 cm, and 25 cm. Squaring the lengths of these sides we get 49, 576, and 625.
Clearly, 49 + 576 = 625 or 72 + 242 = 252 .
Therefore, given triangle is satisfying Pythagoras theorem. So, it is a right triangle. The longest side in a right angled triangle is the hypotenuse.
Therefore length of hypotenuse of this triangle = 25 cm.
ii.Given that sides are 3 cm, 8 cm, and 6 cm. Squaring the lengths of these sides we may get 9, 64, and 36. Clearly, sum of squares of lengths of two sides is not equal to square of length of third side. Therefore given triangle is not satisfying Pythagoras theorem. So, it is not a right triangle
iii.Given that sides are 50 cm, 80 cm, and 100 cm. Squaring the lengths of these sides we may get 2500, 6400, and 10000. Clearly, sum of squares of lengths of two sides is not equal to square of length of third side. Therefore given triangle is not satisfying Pythagoras theorem. So, it is not a right triangle.
iv.Given that sides are 13 cm, 12 cm, and 5 cm. Squaring the lengths of these sides we may get 169, 144, and 25. Clearly, 144 +25 = 169 Or, 122 + 52 = 132.
Therefore given triangle is satisfying Pythagoras theorem. So, it is a right triangle.
The longest side in a right angled triangle is the hypotenuse.
Therefore length of hypotenuse of this triangle = 13 cm.
Solution 2
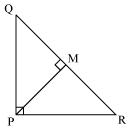

Solution 4
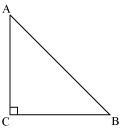
Given that ![]() ABC is an isosceles triangle.
ABC is an isosceles triangle.
Therefore AC = CB
Applying Pythagoras theorem in ABC (i.e. right angled at point C)
Solution 5
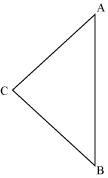
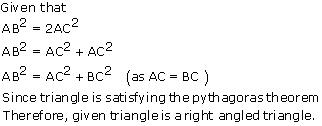
Solution 6
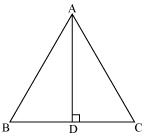
Let AD be the altitude in given equilateral triangle ![]() ABC.
ABC.
We know that altitude bisects the opposite side.
So, BD = DC = a

Since in an equilateral triangle, all the altitudes are equal in length.
So, length of each altitude will be
Solution 8


Solution 9
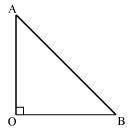

Solution 10
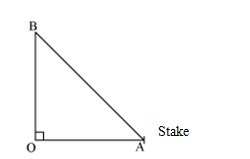
Let OB be the pole and AB be the wire.
Therefore by Pythagoras theorem,
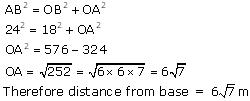
Solution 11
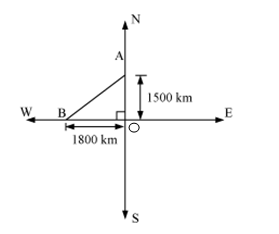

Let these distances are represented by OA and OB respectively.
Now applying Pythagoras theorem
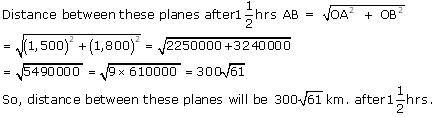
Solution 12
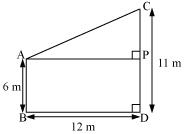
Let CD and AB be the poles of height 11 and 6 m.
Therefore CP = 11 - 6 = 5 m
From the figure we may observe that AP = 12m
In ![]() APC, by applying Pythagoras theorem
APC, by applying Pythagoras theorem
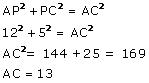
Therefore distance between their tops = 13 m.
Solution 14

Solution 15

Solution 16

Let side of equilateral triangle be a. And AE be the altitude of ![]() ABC
ABC
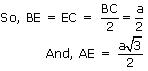
Now, in ![]() ABE by applying Pythagoras theorem
ABE by applying Pythagoras theorem
AB2 = AE2 + BE2
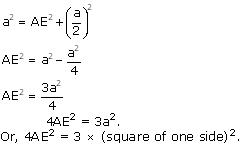
Solution 17
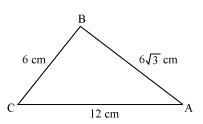
Given that AB = cm, AC = 12 cm and BC = 6 cm
We may observe that
AB2 = 108
AC2 = 144
And BC2 = 36
AB2 +BC2 = AC2
Thus the given triangle ![]() ABC is satisfying Pythagoras theorem
ABC is satisfying Pythagoras theorem
Therefore triangle is a right angled triangle right angled at B
Therefore ![]() B = 90°.
B = 90°.
Hence, (c).
Chapter 6 - Triangles Exercise Ex. 6.6
Solution 3
In ![]() ADB applying Pythagoras theorem
ADB applying Pythagoras theorem
AB2 = AD2 + DB2 (1)
In ![]() ACD applying Pythagoras theorem
ACD applying Pythagoras theorem
AC2 = AD2 + DC2
AC2 = AD2 + (DB + BC)2
AC2 = AD2 + DB2 + BC2 + 2DB x BC
Now using equation (1)
AC2 = AB2 + BC2 + 2BC . BD
Solution 4
In ![]() ADB applying Pythagoras theorem
ADB applying Pythagoras theorem
AD2 + DB2 = AB2
AD2 = AB2 - DB2 (1)
In ![]() ADC applying Pythagoras theorem
ADC applying Pythagoras theorem
AD2 + DC2 = AC2 (2)
Now using equation (1)
AB2 - BD2 + DC2 = AC2
AB2 - BD2 + (BC - BD)2 = AC2
AC2 = AB2 - BD2 + BC2 + BD2 - 2BC. BD
= AB2 + BC2 - 2BC. BD
Solution 10
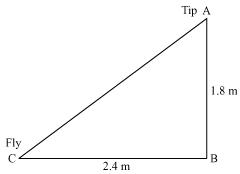
Let AB be the height of tip of fishing rod from water surface. Let BC be the horizontal distance of fly from the tip of fishing rod.
Then, AC is the length of string.
AC can be found by applying Pythagoras theorem in ![]() ABC
ABC
AC2 = AB2 + BC2
AC2 = (1.8)2 + (2.4)2
AC2 = 3.24 + 5.76
AC2 = 9.00
AC =![]() = 3
= 3
Thus, length of string out is 3 m.
Now, she pulls string at rate of 5 cm per second.
So, string pulled in 12 seconds = 12 x 5 = 60 cm = 0.6 m

Let after 12 second Fly be at point D.
Length of string out after 12 second is AD
AD = AC - string pulled by Nazima in 12 seconds
= 3.00 - 0.6
= 2.4
In ![]() ADB
ADB
AB2 + BD2 = AD2
(1.8)2 + BD2 = (2.4)2
BD2 = 5.76 - 3.24 = 2.52
BD = 1.587
Horizontal distance of fly = BD + 1.2
= 1.587 + 1.2
= 2.787
= 2.79 m
Ncert Maths Book Solution Class 10 Chapter 6
Source: https://www.topperlearning.com/ncert-solutions/cbse-class-10-mathematics/mathematics-x/triangles
0 Response to "Ncert Maths Book Solution Class 10 Chapter 6"
Post a Comment