Area of Parallelogram and Triangles Class 9 Ncert Solutions 9.3

NCERT Solutions class 9 maths exercise 9.3 of chapter 9-Areas of parallelogram and triangles

NCERT Solutions class 9 maths exercise 9.3 of chapter 9-Areas of parallelogram and triangles are created here for the purpose of helping the students of 9 class students to boost their preparation of exams. All questions of class 9 maths exercise 9.3 of chapter 9-Areas of parallelogram and triangles are solved by an expert of maths by a step by step method. Here you can study NCERT  solutions of maths and science from class 9 to 12, sample papers, solutions of previous years' question papers. carrier oriented articles.

NCERT Solutions class 9 maths of chapter 9-Areas of parallelogram and triangles

Exercise 9.1 and 9.2- Areas of Parallelogram and Triangles

Exercise 9.3-Areas of Parallelogram and Triangles

Download pdf of NCERT solutions of class 9 maths chapter 9-Areas of Parallelogram and Triangle

PDF-NCERT solutions of class 9 maths chapter 9-Areas of Parallelogram

You can also study NCERT Solutions

Chapter 1-Number system

Chapter 2- Polynomial

Exercise 4.3- Linear equations in two variables

Exercise 4.1 & 4.2- Linear equation in two variables

 Exercise 6.1-Lines and Angles

Exercise 6.2-Lines and Angles

Exercise 6.3-Lines and angles

Exercise 7.1- Triangles

Exercise 7.2- Triangle

Exercise 7.3-Triangle

Exercise 7.4-Triangle

Exercise.9.3- Areas of parallelograms and triangles

NCERT Solutions of Class 9 Science : Chapter 1 to Chapter 15

NCERT Solutions class 9 maths exercise 9.3 of chapter 9-Areas of parallelogram and triangles

Q1.In the given figure,E is any point on the median AD of a ΔABC .Show that ar(ABE) = ar(ACE).

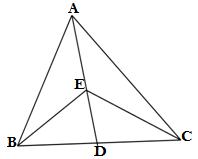
Ans. The median of triagle divides the triangle in two equal parts

AD is given us the median of ΔABC

∴ar ΔABD = arΔACD……(i)

ED is the median of ΔCBE

∴arΔDBE =arDCE……..(ii)

Subtracting equation (ii) from (i)

ar ΔABD – arΔDBE = arΔACD -arDCE

ar(ABE) = ar(ACE), Hence proved

Q2. In a triangle ABC, E is the midpoint of median AD .Show that ar(ΔBED) =1/4 ar(ΔABC).

Ans.

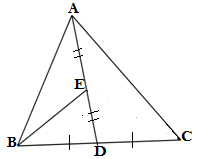
GIVEN: A ΔABC, AD is the median and E is the midpoint of AD

TO PROVE:ar(ΔBED) =1/4 ar(ΔABC)

PROOF: AD is the median of ΔABC (given)

∴ ar(ΔABD) = ar(ΔACD)

⇒ar(ΔABD) =1/2 ar((ΔABC)….(i)

AE = DE (E is the mid point of AD)

∴BE will be the median of ΔABD

ar(BED) = 1/2 ar (ABD)…..(ii)

From equation (i) and equation (ii)

ar(BED) = 1/2 × 1/2 ar((ΔABC)

ar(BED) = 1/4 ar((ΔABC),Hence proved

Q3.Show that diagonal of a parallelogram divide it into four triangles of equal area.

Ans.

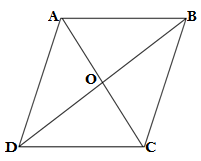
GIVEN: ABCD is a parallelogram and AC and BC are diagonals

TO PROVE: ar(AOB) = ar(AOD) =ar(DOC) =ar(BOC)

PROOF: In ΔADB

DO = BO (diagonal of parallelogram bisect each other)

∴ AO is the median of ΔADB

since the median of the triangle divides the triangle into two equal parts

∴ ar(AOD) = ar(AOB)

DO is the median of ΔADC

∴ar(AOD) =ar(DOC)

BO is the median of ΔABC

∴ar(AOB)  =ar(BOC)

It is clear that

ar(AOB) = ar(AOD) =ar(DOC) =ar(BOC),Hence proved

Q4. In the given figure ,ABC and ABD are two triangles on the same base AB .If line segment CD is bisected by AB at O ,show that ar(ABC) = ar(ABD)

Ans.

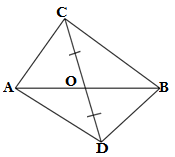
GIVEN: In ABCD ,CD is bisected by AB

CO = DO

TO PROVE: ar(ABC) = ar(ABD)

PROOF: CO = DO (given)

Therefore AO is the median of ΔADC and BO is the median of ΔBDC.

since the median of the triangle divides the triangle into two equal parts

∴ar(AOC)=ar(AOD)…(i)

ar(BOC) = ar(BOD)….(ii)

Adding both equations (i) and (ii)

ar(AOC)+ ar(BOC) =ar(AOD) + ar(BOD)

ar(ABC) = ar(ABD),Hence proved

Latest electronic items,mobiles,laptops and desktops at easy instalments

Q5. D,E and F are the mid points of the sides BC ,CA and AB of a ΔABC. Show that

(i) BDEF is a parallelogram

(ii) ar(DEF) = 1/4 ar(ABC)

(iii) ar(BDEF) = 1/2ar(ABC)

Ans.

GIVEN:D,E and F are the mid points of the sides BC ,CA and AB of a ΔABC

TO PROVE:

(i) BDEF is a parallelogram

(ii) ar(DEF) = 1/4 ar(ABC)

(iii) ar(BDEF) = 1/2ar(ABC)

PROOF: (i) F is the midpoint of AB and E is the mid point of AC

According to mid point theorem

FE∥BC, FE = 1/2(BC)

⇒FE∥BD….(i)

D is the midpoint of BC and E is the mid point of AC

According to the midpoint theorem

DE∥AB, DE = 1/2(AB)

DE∥BF…..(ii)

Equation (i)  and equation (ii) shows that
BDEF is a parallelogram

(ii) BDEF is a parallelogram

ar(DEF) = ar(BDF)…..(i)

DFAE and DFAC will  also be parallelograms

ar(DEF) = ar(AFE)….(ii)

ar(DEF) = ar(DEC)….(iii)

From the figure we have

ar(DEF) + ar(AFE) + ar(DEC) +ar(BDF) = ar(ABC)

From (i),(ii) and (iii) we have

ar(DEF) +ar(DEF)+ar(DEF)+ar(DEF) = ar(ABC)

4 ar(DEF) = ar(ABC)

ar(DEF) = 1/4(ABC), Hence proved

(iii) ar(BDEF) = 1/2ar(ABC)

ar(DEF) = 1/4 ar(ABC) [Proved above]

4ar(DEF)  = ar(ABC)

2 ar(DEF) + 2(DEF) = ar(ABC)

ar(BDEF) + ar(BDEF)  = ar(ABC)

2ar(BDEF) = ar(ABC)

ar(BDEF) = 1/2(arABC),Hence proved

Please follow us on pintrest

Pintrest future study point

Q6. In the given figure ,diagonal AC and BD of quadrilateral ABCD intersect at O such that OB = OD, if AB = CD,then show that

(i) ar(DOC) = ar(AOB)

(ii) ar(DCB) = ar(ACB)

(iii) DA ∥ CB or ABCD is a parallelogram

[ Hint: from D and B , draw perpendiculars to AC]

Ans.

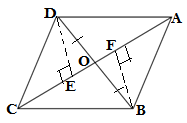
GIVEN: Diagonal AC and BD of quadrilateral ABCD intersect at O such that OB = OD

AB = CD

CONSTRUCTION: Drawing DE ⊥ AC, BF ⊥ AC

TO PROVE:

(i) ar(DOC) = ar(AOB)

(ii) ar(DCB) = ar(ACB)

(iii) DA ∥ CB or ABCD is a parallelogram

PROOF: In ΔDOE and ΔBOF

∠DOE = ∠BOF (vertically opposite angles)

∠DEO = ∠BFO =90°(DE ⊥ AC, BF ⊥ AC)

DO = BO (given)

ΔDOE ≅ ΔBOF (AAS rule)

ar(ΔDOE) = ar(ΔBOF)…..(i)

DE = BF (by CPCT)

In ΔDCE and ΔBFA

DE = BF (proved above)

AB = CD(given)

∠DEC = ∠BFA = 90°(DE ⊥ AC, BF ⊥ AC)

ΔDEC≅ ΔBFA(RHS rule)

ar(ΔDEC) = ar(ΔBFA)….(ii)

Adding equation (i) and (ii)

ar(ΔDOE)+ ar(ΔDEC) = ar(ΔBFA). + ar(ΔBOF)

ar(DOC) = ar(AOB),Hence proved

(ii) ar(DOC) = ar(AOB) [Proved above]

Adding ar(BOC) in both sides

ar(DOC)+ ar(BOC) = ar(AOB) + ar(BOC)

ar(DCB) = ar(ACB)

Q7.D and E are points on sides AB and AC respectively of ΔABC such that ar(DBC) = ar(EBC).Prove that DE||BC.

Ans.

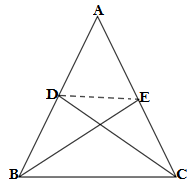
GIVEN: D and E are points on sides AB and AC respectively of ΔABC such that ar(DBC) = ar(EBC)

TO PROVE:DE||BC

PROOF: We know the area of two triangles on the base and between the same parallels are equal,so its converse must also be true

Since ΔDBC and ΔEBC are on the same base BC and between the lines BC and DE

Therefore DE||BC,Hence proved

Q8.XY is a line parallel to side BC of a triangle ABC. If BE||AC and CF||AB meet XY at E and F respectively. show that ar(ABE) = ar(ACF)

Ans.

GIVEN: In figure, XY|| BC,BE||AC and CF||AB

TO PROVE: ar(ABE) = ar(ACF)

PROOF: BE||AC (given)

⇒ BE||YC…..(i)

CF||AB (given)

⇒BX ||AB ….(ii)

XY|| BC (given)

XY is extended upto E and F

⇒EY|| BC….(iii) and XF|| BC …(iv)

From (i) and (ii) it is clear that EYCB is a parallelogram

The parallelogram EYCB and  triangle  ABE are on the same base BE and between the same parallels BE||AC

ar(ΔABE) = 1/2(ar EYCB)…..(v)

From (ii) and (iii) it is clear that XFCB is a parallelogram

The parallelogram XFCB and  triangle  ACF are on the same base CF and between the same parallels BE||AC

ar(ΔACF) = 1/2(ar XFCB)…..(vi)

Since parallelogram EYCB  and XFCB  are on the same base BC and between the same parallels XF|| BC

ar(EYCB)  = ar(XFCB)

From (vi),ar(ΔACF) = 1/2(ar EYCB)….(vii)

From  (v) and (vii) ,we have

ar(ABE) = ar(ACF) ,Hence Proved

Q9.The side AB of a parallelogram ABCD is produced to any point P.A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see the following figure). Show that ar(ABCD) = ar(PBQR)

[Hint: Join AC and PQ. Now compare area(ACQ) ad area(APQ)]

Ans.

GIVEN: ABCD is a parallelogram and AQ||CP ,PBQR is a parallelogram

TO PROVE: ar(ABCD) = ar(PBQR)

CONSTRUCTION: Joining A to C and P to Q

PROOF: The ΔACQ and ΔAPQ are on the same base AQ and between the same parallels AQ||CP

Therefore

ar ΔACQ = ΔAPQ …..(i)

ABC is the common figure in both the triangles ΔACQ  and  ΔAPQ

Subtracting arABC  from both sides of equation (i)

ar ΔACQ – arABC = ΔAPQ- arABC

arΔABC = ar ΔPBQ

Since AC  and  PQ are the diagonals of parallelograms ABCD and PBQR

Therefore

2arΔABC = 2ar ΔPBQ (diagonals of parallelogram bisects it into two equal parts)

ar(ABCD) = ar(PBQR), Hence Proved

NCERT Solutions of  Science and Maths for Class 9,10,11 and 12

NCERT Solutions of class 9 maths

Chapter 1- Number System	Chapter 9-Areas of parallelogram and triangles
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3- Coordinate Geometry	Chapter 11-Construction
Chapter 4- Linear equations in two variables	Chapter 12-Heron's Formula
Chapter 5- Introduction to Euclid's Geometry	Chapter 13-Surface Areas and Volumes
Chapter 6-Lines and Angles	Chapter 14-Statistics
Chapter 7-Triangles	Chapter 15-Probability
Chapter 8- Quadrilateral

NCERT Solutions of class 9 science

Chapter 1-Matter in our surroundings	Chapter 9- Force and laws of motion
Chapter 2-Is matter around us pure?	Chapter 10- Gravitation
Chapter3- Atoms and Molecules	Chapter 11- Work and Energy
Chapter 4-Structure of the Atom	Chapter 12- Sound
Chapter 5-Fundamental unit of life	Chapter 13-Why do we fall ill ?
Chapter 6- Tissues	Chapter 14- Natural Resources
Chapter 7- Diversity in living organism	Chapter 15-Improvement in food resources
Chapter 8- Motion	Last years question papers & sample papers

CBSE Class 9-Question paper of science 2020 with solutions

CBSE Class 9-Sample paper of science

CBSE Class 9-Unsolved question paper of science 2019

NCERT Solutions of class 10 maths

Chapter 1-Real number	Chapter 9-Some application of Trigonometry
Chapter 2-Polynomial	Chapter 10-Circles
Chapter 3-Linear equations	Chapter 11- Construction
Chapter 4- Quadratic equations	Chapter 12-Area related to circle
Chapter 5-Arithmetic Progression	Chapter 13-Surface areas and Volume
Chapter 6-Triangle	Chapter 14-Statistics
Chapter 7- Co-ordinate geometry	Chapter 15-Probability
Chapter 8-Trigonometry

CBSE Class 10-Question paper of maths 2021 with solutions

CBSE Class 10-Half yearly question paper of maths 2020 with solutions

CBSE Class 10 -Question paper of maths 2020 with solutions

CBSE Class 10-Question paper of maths 2019 with solutions

NCERT solutions of class 10 science

Chapter 1- Chemical reactions and equations	Chapter 9- Heredity and Evolution
Chapter 2- Acid, Base and Salt	Chapter 10- Light reflection and refraction
Chapter 3- Metals and Non-Metals	Chapter 11- Human eye and colorful world
Chapter 4- Carbon and its Compounds	Chapter 12- Electricity
Chapter 5-Periodic classification of elements	Chapter 13-Magnetic effect of electric current
Chapter 6- Life Process	Chapter 14-Sources of Energy
Chapter 7-Control and Coordination	Chapter 15-Environment
Chapter 8- How do organisms reproduce?	Chapter 16-Management of Natural Resources

Solutions of class 10 last years Science question papers

CBSE Class 10 – Question paper of science 2020 with solutions

CBSE class 10 -Latest sample paper of science

NCERT solutions of class 11 maths

Chapter 1-Sets	Chapter 9-Sequences and Series
Chapter 2- Relations and functions	Chapter 10- Straight Lines
Chapter 3- Trigonometry	Chapter 11-Conic Sections
Chapter 4-Principle of mathematical induction	Chapter 12-Introduction to three Dimensional Geometry
Chapter 5-Complex numbers	Chapter 13- Limits and Derivatives
Chapter 6- Linear Inequalities	Chapter 14-Mathematical Reasoning
Chapter 7- Permutations and Combinations	Chapter 15- Statistics
Chapter 8- Binomial Theorem	Chapter 16- Probability

CBSE Class 11-Question paper of maths 2015

CBSE Class 11 – Second unit test of maths 2021 with solutions

NCERT solutions of class 12 maths

Chapter 1-Relations and Functions	Chapter 9-Differential Equations
Chapter 2-Inverse Trigonometric Functions	Chapter 10-Vector Algebra
Chapter 3-Matrices	Chapter 11 – Three Dimensional Geometry
Chapter 4-Determinants	Chapter 12-Linear Programming
Chapter 5- Continuity and Differentiability	Chapter 13-Probability
Chapter 6- Application of Derivation	CBSE Class 12- Question paper of maths 2021 with solutions
Chapter 7- Integrals
Chapter 8-Application of Integrals

How to creat and solve algebraic equations like linear and quadratic equations

Achieve hundred percentage marks in maths

NCERT Maths Specific Questions Of Mensuration Class IX & X

Study science notes

Archimedes Principle: Complete detail

Average Speed and Average velocity

Three equation of Motions

Recoil velocity of the gun

Mole concept

The second law of motion

The universal law of gravitational force

Thrust and Pressure : Difference

You can compensate us by donating any amount of money for our survival

Our Paytm NO 9891436286

Area of Parallelogram and Triangles Class 9 Ncert Solutions 9.3

Source: https://futurestudypoint.com/ncert-solutions-class-9-maths-exercise-9-3-of-chapter-9-areas-of-parallelogram-and-triangles/

Share this post